Optische Linsen werden in einer Vielzahl von Anwendungen verwendet, um einfallendes Licht oder allgemein elektromagnetische Strahlung zu manipulieren. Aufgrund des Brechungsindex der Linse kann die Strahlung abhängig von der Funktion der Linse z.B. fokussiert oder gestreut werden. Dreidimensionale (3D) Simulationen der Wechselwirkung von elektromagnetischer Strahlung und Linsen, welche häufig aus dielektrischen Materialien gefertigt sind, können beim Entwurf einzelner Linsen und Linsensystemen oder bei der Optimierung dieser verwendet werden, ohne dass kostspielige Prototypen konstruiert und langwierige Experimente durchgeführt werden müssen. Im Folgenden werden die Kernpunkte von einer 3D Simulation optischer Linsen erläutert.
Dielektrika
Dielektrika sind Materialien, die polarisiert werden können, wenn ein elektrisches Feld angelegt wird. Üblicherweise werden sie als elektrische Isolatoren eingesetzt, z.B. in Kondensatoren. In PICLas können dielektrische Materialien in elektrostatischen oder elektrodynamischen Simulationen verwendet werden. Im ersten Fall kann die Poisson-Gleichung, die das elektrische Potential beschreibt, unter Berücksichtigung dielektrischer Materialien gelöst werden. Im zweiten Fall müssen die vollen Maxwell-Gleichungen gelöst werden, die die Wechselwirkung elektromagnetischer Felder berücksichtigen. In PICLas werden Discontinuous Galerkin-Methoden höherer Ordnung(DGSEM) sowohl für Poisson- als auch für Maxwell-Gleichungen in Kombination mit dielektrischen Materialien verwendet. Diese Methoden kombinieren klassische Merkmale, die typischerweise Finite-Volumen- und Finite-Elemente-Methoden zugeschrieben werden, nämlich numerische Füsse zwischen benachbarten Simulationselementen und polynomialen Basisfunktionen, die die Lösung innerhalb von Elementen darstellen. Für weitere Details zur Theorie und numerischen Implementierung siehe Pfeiffer et al. (elektrostatisch) und Copplestone (elektrodynamisch) in der Referenzliste.
3D Simulationssetup
In der Simulation wird eine quaderförmige Domäne von 1,3 m × 0,4 m × 0,4 m mit unstrukturierten Elementen verwendet. Die rotationssymmetrische optische Linse mit konstanten dielektrischen Eigenschaften und einem Durchmesser von 20 cm befindet sich in der Nähe des Zentrums. Links vor der Linse befindet sich ein elektromagnetischer Dipol, der ein Signal mit einer konstanten Frequenz von 80 GHz aussendet. Der Maxwell-Solver höherer Ordnung von PICLas wird aufgrund der hervorragenden Skalierbarkeit und Performance auf HPC-Systemen für dieses Setup verwendet. In der Simulation werden insgesamt 168 856 Elemente verwendet und der Polynomgrad N der Lösung in jedem Element wird zwischen 7 und 11 variiert (pro Simulation wird ein globaler Polynomgrad gewählt), was einer räumlichen Konvergenzordnung von O(N + 1) entspricht, während die zeitliche Ordnung bei 4 festgehalten wird.
Da in der Simulation ein explizites Zeitintegrationsverfahren verwendet wird, muss die höchste Geschwindigkeit des Systems, die Lichtgeschwindigkeit, in jeder Gitterzelle aufgelöst werden. Das Kriterium, das dies erzwingt, ist die sogenannte CFL-Bedingung, die die Entfernung begrenzt, die Information in einem Zeitschritt zurücklegen darf. Aufgrund der sehr kleinen Elemente in der Nähe der Linsenecken, wird ein sehr kleiner Zeitschritt erforderlich. Im Wesentlichen werden die erforderlichen Rechenkosten der Simulation immer erhöht, wenn winzige geometrische Merkmale aufgelöst werden müssen.
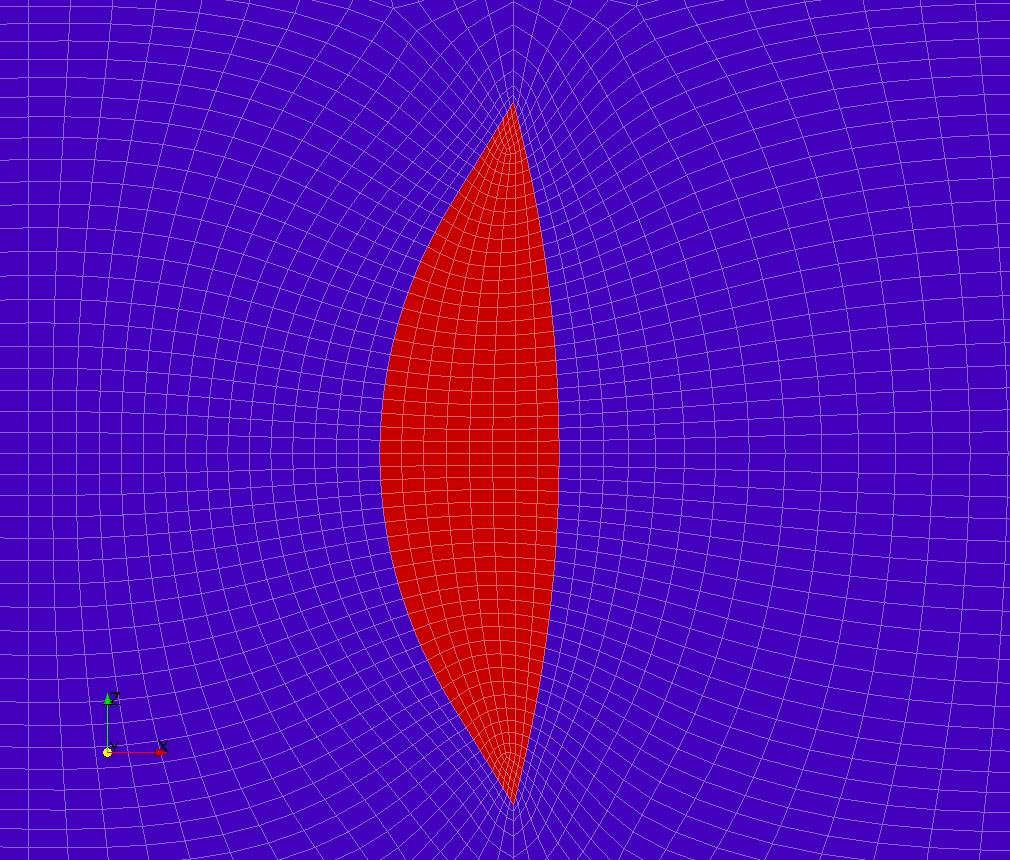
Zoom auf die Linse nahe der Mitte der Domäne um die Größe und Verteilung der dielektrischen Elemente zu verdeutlichen. Der rote Bereich zeigt den Bereich des Dielektrikums. Außerhalb dessen wird die Permittivität von Vakuum verwendet.
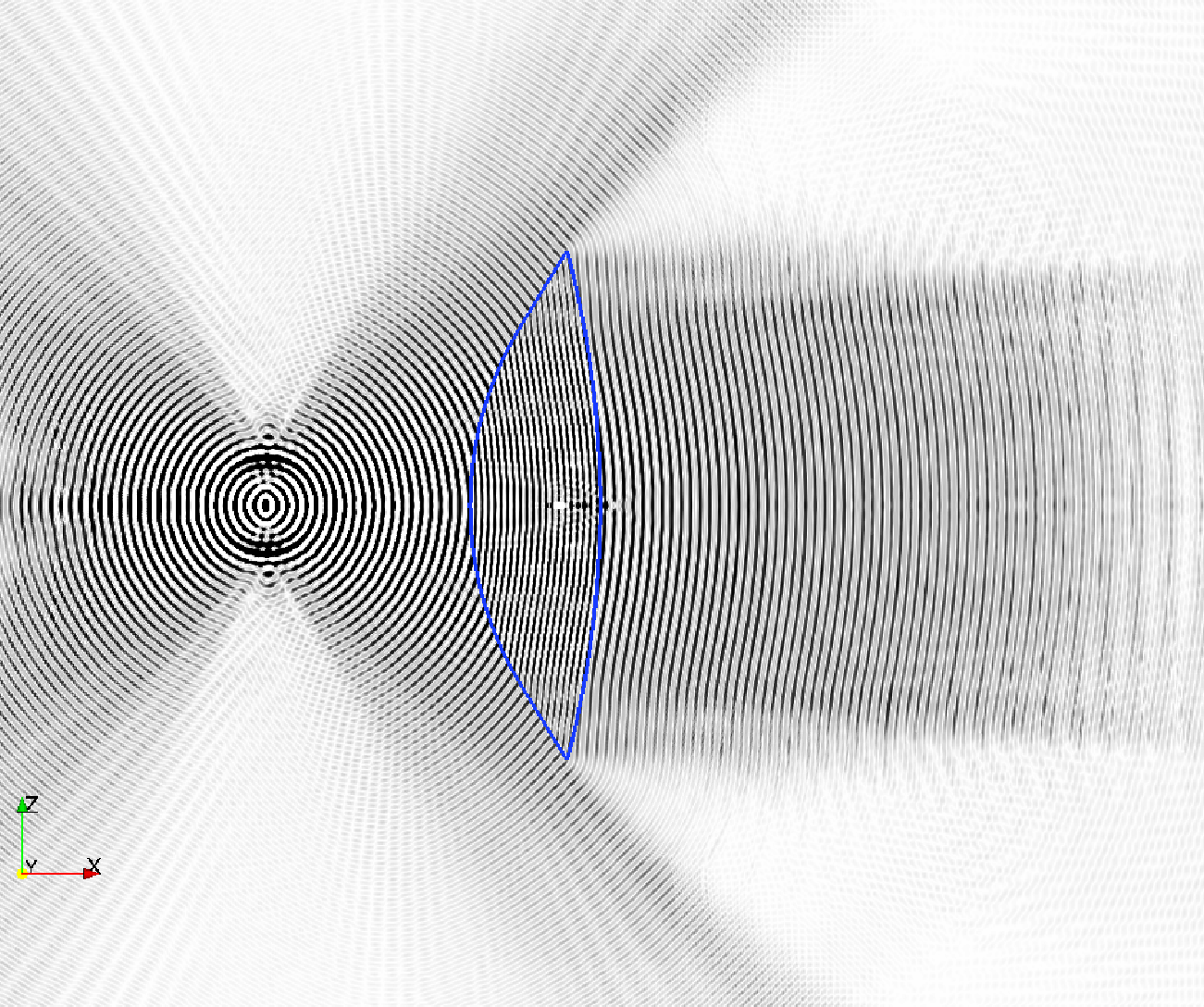
Das Bild rechts zeigt die Verteilung der elektrischen Feldstärke in und um die Linse, welche einen starken Effekt auf die einfallende elektromagnetische Strahlung des Dipols hat und zeigt eine deutliche Verringerung der Wellenlänge innerhalb der Linse aufgrund des dielektrischen Materials. Dies hat zur Folge, dass die Auflösung innerhalb des dielektrischen Bereichs erhöht werden muss, um die verringerte Wellenlänge adäquat aufzulösen.
Ausblick
Bei den hier verwendeten expliziten Verfahren wird die Stabilität des gesamten Verfahrens durch den Zeitschritt in der kleinsten Zelle bedingt. Diese kleinen Elemente sind in der Regel bei komplexen 3D Gittern anzutreffen, wenn Hinterschneidungen oder Ähnliches vergittert werden müssen oder wenn kleine geometrische Details aufgelöst werden sollen. Dies kann zu extrem hohen Simulationskosten in Form von Rechenzeit führen, vor allem bei großen Systemen in denen kleine Wellenlängen aufgelöst werden müssen. Wenn man die lokalen Effekte von kleinen geometrischen Objekten vernachlässigen kann, ist es möglich mit Hilfe von impliziten Methoden den Zeitschritt zu vergrößern ohne dass die Stabilität des Verfahrens beeinträchtigt wird. Auf der anderen Seite benötigt ein impliziter Zeitschritt höhere Rechenkosten als ein expliziter Zeitschritt, sodass ein gewisses Verhältnis zwischen dem expliziten und impliziten Zeitschritt erreicht werden muss um insgesamt schneller zu einer Lösung zu gelangen. Außerdem ist es möglich mit einem sehr großen Zeitschritt zu beginnen und diesen dann sukzessive zu verkleinern bis die gewünschte Lösungsqualität erreicht ist. In PICLas sind verschiedene implizite Verfahren zur Lösung der Maxwell-Gleichungen implementiert (voll- und teil-implizit), welche bereits erfolgreich an technischen Anwendungsfällen getestet wurden, siehe dazu Ortwein (2019).
Mehr Informationen zu den zugrunde liegenden Theorien und Modellierungen:
- Pfeiffer, M., Hindenlang, F., Binder, T., Copplestone, S.M., Munz, C.D. and Fasoulas, S., (2019). A particle-in-cell solver based on a high-order hybridizable discontinuous Galerkin spectral element method on unstructured curved meshes. Computer Methods in Applied Mechanics and Engineering, 349, pp.149-166.
- Copplestone, S.M., (2019). Particle-based Numerical Methods for the Simulation of Electromagnetic Plasma Interactions. Verlag Dr. Hut.
- Ortwein, P., (2019). Implicit Time Integration Strategies for a Particle-in-Cell Solver. Verlag Dr. Hut.