Der Feldlöser von PICLas verwendet discontinuous Galerkin Methoden hoher Ordnung, um die Poisson und Maxwell-Gleichungen unter Berücksichtigung von dielektrischen Materialen zu lösen. Diese Verfahren kombinieren die vorteilhaften Eigenschaften von klassischen Methoden wie dem Finite-Volumen und Finite-Elemente Verfahren bei denen numerische Flüssen zwischen benachbarten Elementen bzw. polynomiale Basisfunktionen in den Elementen verwendet werden. Mehr Informationen bezüglich der Theorie und numerischen Implementierung können unter Pfeiffer et al. für den elektrostatischen und unter Munz et al. (2014) für den elektromagnetischen Fall in der Referenzliste gefunden werden.
Vorteile von Verfahren Hoher Ordnung für die Simulation von Elektro(-dynamischen) Phänomenen
Verfahren hoher Ordnung weisen klare Vorteile gegenüber Verfahren niedriger Ordnung auf, welche in der Regel eine Raum- und Zeitordnung von zwei aufweisen, bei denen eine Verdoppelung der Auflösung in Raum und Zeit jeweils den numerischen Fehler um einen Faktor 4 verkleinern. Der Grund dafür ist, dass der Fehler err∝Δxa mit der räumlichen Gitterschrittweite Δx skaliert, wobei der Exponent a die räumliche Ordnung des Verfahren darstellt und typischerweise als Konvergenzordnung bezeichnet wird. Im Prinzip kann der Faktor a mit Hilfe von Verfahren hoher Ordnung drastisch erhöht werden, sodass der selbe Fehler wie beim Verfahren niedriger Ordnung erreicht wird, nur eben mit deutlich geringerer Auflösung. Die Methoden, die hier Anwendung finden, wurden speziell dafür entwickelt auf Höchstleistungsrechnern unter Zuhilfenahme von einer Vielzahl an CPU-Prozessorkernen möglichst effizient zu sein. Dies ermöglicht Simulationen im großen Maßstab, wobei sehr kleine Wellenlängen aufgelöst werden können (hohe Frequenzen). Im Folgenden werden zwei Fälle beschrieben, bei denen Verfahren hoher Ordnung Verwendung finden und ihr hohes Anwendungspotential unter Beweis stellen.
Der Elektrostatische Fall: Kugel mit Dielektrikum
Die Poisson-Gleichung steht im Zentrum der elektrostatischen Modellierung in PICLas,
∇2Φ = -ρ/ε
welche das elektrostatische Potential Φ mit der Ladungsdichteverteilung im Raum ρ und der Permittivität ε der Umgebung in Relation stellt. Daraus lässt sich eine Gleichung für die elektrische Feldstärke E ableiten,
∇ · E = ρ/ε
Die Gleichungen werden in PICLas mit Hilfe eines modernen hybriden discontinuous Galerkin Ansatzes gelöst, Details dazu finden sich in Pfeiffer et al. (2019). Das Verfahren verbindet geringe numerische Fehler mit einer guten Skalierbarkeit auf HPC Systemen.
Für den ersten Testfall wird eine Kugel betrachtet in der sich ein Dielektrikum befindet. Zusätzlich wird eine äußere konstante Spannung angelegt. Das Bild zeigt die dreidimensionale Geometrie des Simulationsgebiets in dem die Kugel platziert wird.
Die dielektrische Kugel mit konstanter Permittivität εin ist von einem Medium mit εout vollständig umgeben. Das Gitter besteht aus 56 gekrümmten Hexaedern und das Materialinterface liegt exakt zwischen zwei benachbarten Elementen, sodass der Sprung in den Materialeigenschaften direkt auf dem Interface liegt.
Die numerische und analytische Lösung werden hinsichtlich des elektrischen Potentials Φ und dessen erste räumliche Ableitung, des elektrischen Feldes E, verglichen und weisen eine hervorragende Übereinstimmung auf. Der linke Plot repräsentiert ein moderates Verhältnis εin/εout wohingegen der rechte Plot ein extremes Gefälle in den Permittivitäten aufweist um zu zeigen, dass dies vom Löser ohne Probleme berücksichtigt werden kann.
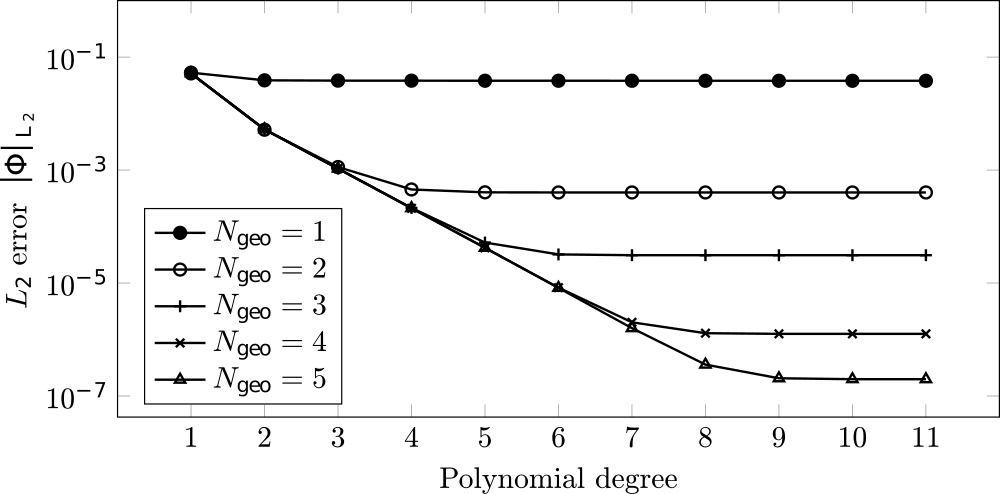
Um die Konvergenzeigeschaften des Lösers zu untersuchen, wird die L2 Norm, welche die Wurzel des quadratisch gemittelten Fehlers als Abweichung zwischen numerischer und analytischer Lösung darstellt, betrachtet. Zusätzlich werden unterschiedliche Polynomgrade, wobei N dem Grad des Lösungspolynoms in jeder Zelle und NGeo dem geometrischen Polynomgrad, der das Gitter repräsentiert, entspricht, im Folgenden genauer betrachtet. Der Wert NGeo=1 entspricht dabei einem linearen Gitter, bei dem die Gitterknotenpunkte durch Geraden verbunden sind. Die Konvergenzverläufe zeigen für eine fixe Anzahl an Elementen, dass ein erhöhter Polynomgrad den numerischen Fehler signifikant reduzieren kann, wenn der geometrische Polynomgrad hoch genug ist.
L2 Fehler in Abhängigkeit des Polynomgrades N.
Wichtig zu nennen ist, dass die benötigte Zeit zum Lösen des Problems beim Verfahren hoher Ordnung signifikant verkleinert werden kann im Vergleich zum äquivalent aufgelösten Problem mit einem kleineren Polynomgrad. Zusätzlich erlauben die guten Skalierungseigenschaften des Verfahrens hoher Ordnung eine Ausführung auf HPC Clustern mit einer Vielzahl an CPU Kernen, was das Gesamtverfahren sehr effizient macht. Nähere Details zu all diesen Punkten können in Pfeiffer et al. (2019) nachgeschlagen werden.
Der Elektrodnynamische Fall: Ebene Welle in einer vollperiodischen Box
Im elektrodynamischen Szenario werden die Maxwell-Gleichungen relevant, da nun die Ausbreitungsgeschwindigkeit von elektromagnetischen Wellen (Lichtgeschwindigkeit c) wichtig wird,
∇ · E = ρ/ε
∇ · B = 0
∂E/∂t = c2/(εrµr) ∇×B - j/ε
∂B/∂t = -∇ · E
mit den elektromagnetischen Feldern E und B, welche mit einem discontinuous Galerkin Verfahren (DGSEM) hoher Ordnung gelöst werden. Dieses Verfahren ist extrem effizient und parallelisierbar auf HPC Clustern bis hin zu tausenden von Kernen. Dies wird durch die geschickte Kombination von Eigenschaften aus Finite-Elemente und Finite-Volumen Verfahren erreicht. Weitere Informationen und Details zur Implementierung finden sich in Munz et al. (2014).
Im folgenden Beispiel, Hintergründe dazu finden sich in Copplestone (2020), wird eine elektromagnetische ebene Welle betrachtet, die sich diagonal durch ein vollperiodisches Gebiet bewegt. Die Simulationsdomain besteht aus 44=64 Elementen und die Welle besitzt eine eindeutige Wellenlänge.
Die rote Kurve verdeutlicht den Effekt eines variablen Polynomgrades auf einem fixen Gitter (fest Anzahl der Elemente) und zeigt sogenannte spektrale Konvergenz (p-Konvergenz). Das bedeutet, dass der Fehler mit steigendem Polynomgrad immer schneller gegen Null tendiert wenn das Verfahren von niedriger Ordnung zu hoher Ordnung verschoben wird. Die beiden schwarzen Kurven zeigen den Fehlerverlauf für einen fixen Polynomgrad N, bei dem die Anzahl der Gitterelemente und damit die räumliche Auflösung variiert wird (h-Konvergenz). Im Plot werden 5. und 11. Ordnung exemplarisch dargestellt.
Implizite Zeitintegration
Bei den hier verwendeten expliziten Verfahren wird die Stabilität des gesamten Verfahrens durch den Zeitschritt in der kleinsten Zelle bedingt. Diese kleinen Elemente sind in der Regel bei komplexen 3D Gittern anzutreffen, wenn Hinterschneidungen oder Ähnliches vergittert werden müssen oder wenn kleine geometrische Details aufgelöst werden sollen. Dies kann zu extrem hohen Simulationskosten in Form von Rechenzeit führen, vor Allem bei großen Systemen in denen kleine Wellenlängen aufgelöst werden müssen. Wenn man die physikalischen Effekte von kleinen geometrischen Objekten vernachlässigen kann, ist es möglich mit Hilfe von impliziten Methoden den Zeitschritt zu vergrößern ohne dass die Stabilität des Verfahren beeinträchtigt wird. Auf der anderen Seite benötigt ein impliziter Zeitschritt allerdings höhere Rechenkosten als ein expliziter Zeitschritt, sodass ein gewisses Verhältnis erreicht werden muss um insgesamt schneller zu einer Lösung zu gelangen. Außerdem ist es möglich mit einem sehr großen Zeitschritt zu beginnen und diesen dann sukzessive zu verkleinern bis die gewünschte Lösungsqualität erreicht ist. In PICLas sind verschiedene implizite Verfahren zur Lösung der Maxwell-Gleichungen implementiert (voll- und teil-implizit), welche bereits erfolgreich an technischen Anwendungsfällen getestet wurden, siehe dazu Ortwein (2019).
Mehr Informationen zu den zugrunde liegenden Theorien und Modellierungen:
- Pfeiffer, M., Hindenlang, F., Binder, T., Copplestone, S.M., Munz, C.D. and Fasoulas, S., (2019). A particle-in-cell solver based on a high-order hybridizable discontinuous Galerkin spectral element method on unstructured curved meshes. Computer Methods in Applied Mechanics and Engineering, 349, pp.149-166.
- Copplestone, S.M., (2019). Particle-based Numerical Methods for the Simulation of Electromagnetic Plasma Interactions. Doktorarbeit, Verlag Dr. Hut.
- Ortwein, P., (2019). Implicit Time Integration Strategies for a Particle-in-Cell Solver. Doktorarbeit, Verlag Dr. Hut.
- C.-D. Munz, M. Auweter-Kurtz, S. Fasoulas, A. Mirza, P. Ortwein, M.
Pfeiffer, and T. Stindl (2014). Coupled Particle-In-Cell and Direct Simulation Monte Carlo method for simulating reactive plasma flows”. Comptes Rendus Mécanique 342.10-11, pp. 662–670.