The field solver in PICLas utilizes higher-order discontinuous Galerkin methods for both Poisson's and Maxwell's equations in combination with dielectric materials. These methods combine classical features that are typically attributed to finite-volume and finite-element methods, namely numerical surface fluxes between adjacent simulation cells or elements and polynomial basis functions that represent the solution within. For more details on the theory and numerical implementation, see Pfeiffer et al. for the electrostatic and Munz et al. (2014) for the electrodynamic case in the list of references.
The Advantages of using High-order Methods for the Simulation of Electro(-dynamic) Phenomena
High-order methods offer distinct advantages when compared with their low-order counterpart, which usually exhibit a temporal and spatial order of convergence of two. This means that when the disretization in time or space is doubled, the numerical error drops by a factor of four, because the error scales with the grid resolution by err∝Δxa, where the error is proportional to the grid spacing Δx and the exponent a. The latter is commonly termed the order of convergence of the scheme. Essentially, with high-order methods, the factor a can drastically be increased. Therefore, the same numerical error can be achieved but with much less resolution as compared with the low-order method. The methods used here have specifically been designed and further developed to run efficiently on high-performance systems utilizing a great number of CPU processors, which allows the simulation of large-scale applications with very small wave lengths (high frequencies). In the following, two cases are illustrated where higher-order methods have been utilized showing their high potential.
The Electrostatic Case: Dielectric Sphere
Central to the electrostatic modelling in PICLas is Poisson's equation,
∇2Φ = -ρ/ε
which relates the electrostatic potential Φ to the charge density distribution ρ and the permittivity ε of the environment. Furthermore, the electric field E can be obtained from,
∇ · E = ρ/ε
The equations above are solved using a modern hybridizable discontinuous Galerkin
method as described in Pfeiffer et al. (2019). It combines low numerical errors with good scalability on HPC systems.
For the first test case, a dielectric sphere is considered on which an externally applied constant electric field takes effect. The picture shows the three-dimensional geometry of the simulation domain, into which the sphere is placed.
The dielectric sphere with a permittivity of εin is submerged into a surrounding environment that has a permittivity of εout. The mesh consists of 56 curvilinear, hexahedral elements and the material interface is positioned exactly at the interface between the elements.
The numerical and analytical solution are compared and exhibit excellent agreement for the electric potential Φ and the first derivative, which is the electric field E. The plot on the left shows a moderate ratio of εin/εout, whereas the right plot features an extremely high ratio to show that the solver experiences no problems when dealing with such big jumps in the material properties across the dielectric interface.
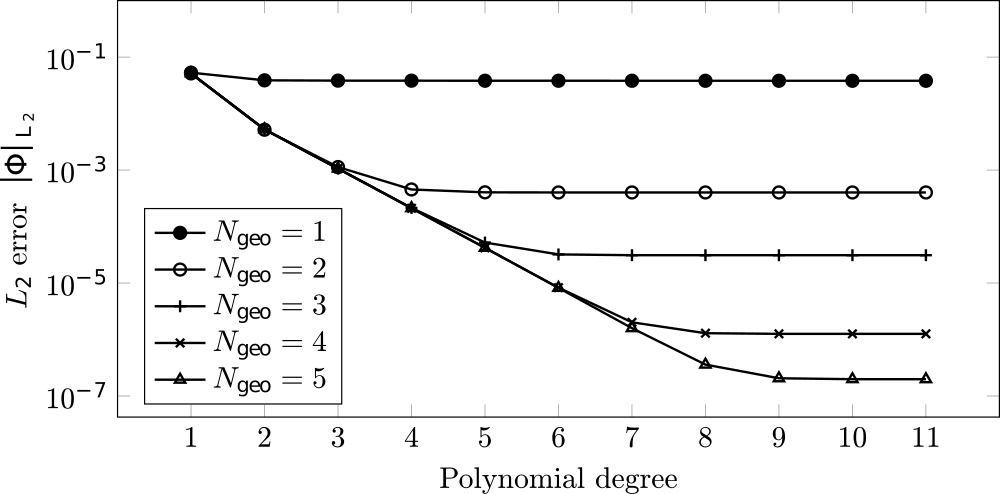
To examine the convergence properties of the solver, the L2 norm, which resembles the square root error between the numerical and the analytical solution, is determined. Furthermore, different polynomial degrees, where N corresponds to the solution polynomial and NGeo to the geometrical polynomial degree where NGeo=1 corresponds to a linear geometry, are considered. The convergence plot shows that for a fixed number of elements, an increased polynomial degree reduces the error as long as the geometry is sufficiently described a high enough polynomial degree.
Important to note is that the time required for solving the problem using a high polynomial requires much less time than the equivalently resolved problem where a low order is used. Additionally, the good scaling properties of the high-order scheme on multi-processor platforms renders the overall method highly efficient. Details on all these topics are found in Pfeiffer et al. (2019).
The Electrodynamic Case: Plane wave in a 3D fully periodic domain
In the electrodynamic scenario, Maxwell's equations become relevant as the finite propagation velocity of electromagnetic radiation, the speed of light c, becomes relevant
∇ · E = ρ/ε
∇ · B = 0
∂E/∂t = c2/(εrµr) ∇×B - j/ε
∂B/∂t = -∇ · E
where the electromagnetic fields E and B, respectively, are solved using a high-order discontinuous Galerkin method (DGSEM). This scheme is highly efficient and parallelizable on HPC clusters up to thousands of cores. This is achieved by combining the features of classic finite-element and finite-volume methods and details on the implementation can be found in Munz et al. (2014).
In the following example, details of which are found in Copplestone (2020), an electromagnetic plane wave travels in a periodic simulation domain that is made up of 44=64 elements. The wave has a single wavelength and moves diagonally in the domain.
The red curve shows the effect of varying the polynomial degree on a fixed mesh, showing a fast drop of the error when the polynomial degree is increased and a shift from a low-order scheme to a high-order method occurs (spectral convergence). The two black lines indicate the error of convergence for a fixed polynomial degree, where the number of grid cells is varied, which is termed h-convergence. Here a 5th and an 11th order of convergence are shown exemplary.
Implicit Time Integration
Due to numerical stability, the smallest mesh cell dictates the time step in a scheme with explicit time integration. These small elements are usually encountered in complex three-dimensional applications where small geometrical features are to be resolved. This can lead to heavy computational demand when solving large systems in combination with high frequencies (small wavelengths). When the physical effect of small geometrical features is negligible, implicit methods can mitigate the computational costs by increasing the global time step because these methods lift the stability restriction with respect to the time step. On the other hand, a single implicit time step requires more computational resources as compared with an explicit one. Therefore, the speed-up is only achieved if the time step is increased correspondingly. Additionally, a large time step can be used as a starting point, which is then successively increased until the desired solution quality is achieved instead of beginning the the very small time step of the explicit simulation. PICLas offers such a fully implicit method for solving Maxwell's equations and has already been applied successfully to technical applications, see Ortwein (2019).
More information about the underlying theory and modelling can be found here:
- Pfeiffer, M., Hindenlang, F., Binder, T., Copplestone, S.M., Munz, C.D. and Fasoulas, S., (2019). A particle-in-cell solver based on a high-order hybridizable discontinuous Galerkin spectral element method on unstructured curved meshes. Computer Methods in Applied Mechanics and Engineering, 349, pp.149-166.
- Copplestone, S.M., (2019). Particle-based Numerical Methods for the Simulation of Electromagnetic Plasma Interactions. PhD Dissertation, Verlag Dr. Hut.
- Ortwein, P., (2019). Implicit Time Integration Strategies for a Particle-in-Cell Solver. PhD Dissertation, Verlag Dr. Hut.
- C.-D. Munz, M. Auweter-Kurtz, S. Fasoulas, A. Mirza, P. Ortwein, M.
Pfeiffer, and T. Stindl (2014). Coupled Particle-In-Cell and Direct Simulation Monte Carlo method for simulating reactive plasma flows”. Comptes Rendus Mécanique 342.10-11, pp. 662–670.